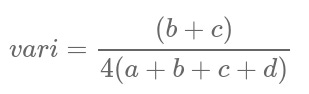Classificação Multirrótulo: Calculando Similaridades entre Rótulos - Parte 11

https://pixabay.com/illustrations/ai-artificial-intelligence-humanoid-7265469/

Oi pessoal!!! Hoje darei continuidade à nossa série de artigos e mostrarei alguns detalhes importantes que poderão ser úteis a vocês para outros projetos também. Aliás, tudo o que eu escrevi nessa série, vocês podem sempre considerar quando forem criar novos projetos!

Organização do pensamento, do fluxo de processo do código, separar os escopos, etc., tudo isso é importante ser feito, preferencialmente antes de começar a codar. Nem sempre isso acontece e aí a gente acaba perdendo um tempão da vida pra organizar tudo depois, é retrabalho!!!! Convenhamos que ninguém gosta muito de ficar refazendo coisas.

Nesse ponto, eu concordo com o pessoal da Engenharia de Software, afinal eles sempre pensam nisso tudo antes de sair codando, e tem disponíveis diversas técnicas para isso. Tudo bem, não precisam usar nada elaborado ou complexo, uma Figura simples que você consiga desenhar e que reflita como as coisas devam ocorrer já ajuda muito!

ORDEM DE PRIORIDADES DE OPERADORES MATEMÁTICOS

Algo importante que eu não mencionei ainda é sobre a ordem em que os operadores matemáticos são executados e que faz toda a diferença na hora de transformarmos as medidas de similaridades em funções no R.

Se você já está familiarizado com este assunto pode pular este tópico, mas caso nunca tenha ouvido falar, leia com bastante atenção. Novamente, vamos pegar a medida VARI, vejam a construção dela:

VARI

O numerador é (b + c) e o denominador é 4 * ( a + b + c + d) e vari é o resultado da divisão do numerador pelo denominador. No artigo passado mostrei duas versões de como fica essa medida, a primeira onde eu separei cada parte desse cálculo, como se estivesse fazendo à mão, e a segunda onde coloquei tudo em uma linha só. Vou repetir aqui apenas a segunda versão aqui:

vari_v2 <- function(a, b, c, d){
  return((b+c) / (4 * (a + b + c + d)))
}

Vocês perceberam que eu adicionei vários parênteses? Por que isso? Será que se apenas digitássemos da forma como vimos ali em cima não daria certo? Bom, não vai dar certo, gente! Vamos fazer um cálculo simples aqui. Suponha que a = 1, b = 5, c = 8 e d = 3. Vari ficará assim

vari = ( (b+c) / (4 * (a + b + c + d) ) )

vari = ( ( 5 + 8 ) / ( 4 *  ( 1 + 5 + 8 + 3 ) ) 

vari = 0,191176471

Fazendo na mão é fácil né, mas no computador não é assim. Qual operador vocês acham que será operado primeiro no computador? Isto é, qual operação será executada primeiro? A soma? A divisão? O numerador? O denominador? Na minha resolução manual eu fiz várias contas de uma vez só, mas no computador não é assim!!!

Apesar de toda a evolução tecnológica, a maioria das nossas CPUs ainda são construídas com instruções básicas que em sua maioria calculam apenas UM OPERADOR POR VEZ. Caso esteja curioso sobre o assunto, recomendo ler estes artigos aqui.

Sendo assim, não tem como o computador calcular tudo de uma vez só e ele precisará saber quem é que vai ser executado primeiro nesse monte de operações que tem aí. A maioria das linguagens de programação segue a seguinte prioridade de execução de operadores:

1. Parênteses

2. Funções pré-definidas (como raíz quadrada, potência, etc.)

3. Multiplicação ou Divisão

4. Soma ou Subtração

5. Operadores relacionais: igual, diferente, maior que, menor que, maior ou igual que, menor ou igual que

6. Operador Lógico NOT

7. Outros operadores lógicos (and, or, etc.)

Assim sendo, temos que obedecer a essas regras e garantir que a função será corretamente calculada pela linguagem de programação. Dessa forma, em nosso caso, será executado o primeiro parêntese que aparece na instrução, ou seja, o numerador (b+c):

resultado1 = b + c

Ah sim! Já estava quase esquecendo, a leitura da instrução é feita da esquerda para a direita, então, a análise é feita nessa direção, daí é calculado a prioridade que aparece primeiro nessa leitura.

Bom, continuando!! Depois de executado o primeiro parêntese, será executado o segundo parênteses, só que dentro desse segundo parênteses tem outro parênteses. Então, a prioridade é executar primeiro todos os parênteses internos até chegar no parêntese mais externo. Dessa forma calcula-se (a + b + c + d), isto é:

resultado2 = a + b

resultado3 = resultado2 + c

resultado4 = resultado3 + d

Somente depois multiplica-se 4 pelo resultado dessa conta:

resultado5 = 4 * resultado4

E, por fim é feita a divisão:

vari = resultado1 / resultado5

Se você não colocar o parênteses em (4 * ( a + b + c + d) ) o resultado será diferente pois o computador vai achar que é pra dividir (b + c ) por 4 e não que é para dividir (b + c ) por todo o restante! Quer uma prova do que estou falando? Vou executar a função vari com e sem parênteses aqui no meu script R, vejam:

vari_correta <- function(a, b, c, d, n){
  return((b+c) / (4 * (a + b + c + d)))
}

vari_incorreta <- function(a, b, c, d, n){
  return( (b+c) / 4 * (a + b + c + d))
}

a = 1
b = 5
c = 8
d = 3

vari_correta(a,b,c,d)
vari_incorreta(a,b,c,d)

Olhem só para esses resultados! Tudo isso pois não coloquei parênteses no lugar certo! Imaginem o estrago disso se alguém usar essa função para algo importante como, por exemplo, mensurar o nível de similaridade entre rótulos para descobrir novos insigths sobre os dados? É DESASTROSO!!!!

Algo tão simples, mas tão impactante! Portanto, não negligenciem o básico!

Assim sendo pessoal, vamos fazer a transformação, ou tradução/conversão, das medidas de similaridades, corretamente para as funções de similaridades para o R. Tem uma outra coisa que também precisamos considerar ao fazer essas traduções. Vou pegar agora a medida cosseno que usa a função pré-definida de raiz quadrada:

Cosseno

Como poderíamos convertê-la, ou traduzi-la? Vejamos como devemos calcular:

1. (a + b)

2. (a + c)

3. multiplicar a + b com a + c -->  (a + b ) * ( a + c)

4. calcular a raiz quadrada do resultado da multiplicação --> raiz((a + b ) * ( a + c))

5. encontrar a potência do resultado da raiz quadrada --> potencia(raiz((a + b ) * ( a + c)))

6. dividir a pelo resultado da potência --> a /potencia(raiz((a + b ) * ( a + c))

Então temos a função de similaridade do cosseno:

cosseno <- function(a, b, c){
  return( a /  ( ( sqrt( (a+b) * (a+c) ) ) ^ 2  ) )
}

Vamos calcular na mão rapidinho:

cosseno = ( 1 / ( ( sqrt( (1+5) * (1+8) ) ) ^ 2 ) ) = 0.01851852

Se você copiar essa linha no seu script R obterá exatamente o mesmo resultado. Se quiser testar a função, faça da seguinte forma e também obterá o mesmo resultado:

a = 1
b = 5
c = 8
d = 3

cosseno(a,b,c)

0.01851852

No entanto, a função SQRT pode dar problema com números negativos e isto pode dar erro no cálculo da medida. Faça o seguinte teste:

a = -1
b = 5
c = -8
d = 3

cosine(a,b,c)

O resultado será:

[1] NaN
Warning message:
In sqrt((a + b) * (a + c)) : NaNs produzidos

Para evitar esse problema, usamos a função ABS (valor absoluto) em todas as funções que utilizam SQRT. Assim conseguiremos calcular corretamente os valores para essas medidas de similaridades. A função ficará então da seguinte forma:

cosseno <- function(a, b, c){
  return( a /  ( ( sqrt( abs( (a+b) * (a+c) ) ) ) ^ 2  ) )
}

Agora sim está certo! Então, atentem-se para este detalhe quando estiverem trabalhando com esse tipo de cálculo! A função ABS deve ser incluída no trecho do cálculo onde o problema provavelmente ocorrerá. Não adianta colocá-la só no fim do cálculo pois também não computará corretamente ok.

FINALIZANDO

Acredito que toquei num ponto importante no artigo de hoje! Agora que já sabemos como converter corretamente as medidas de similaridades para funções no R, já podemos partir para o próximo passo. Vejo vocês no próximo artigo.

Este artigo foi escrito por Elaine Cecília Gatto - Cissa e publicado originalmente em Prensa.li.