Classificação Multirrótulo: Calculando Similaridades entre Rótulos - Parte 12
Oi pessoal! Estou de volta depois de uns dias. Espero terminar esta série neste mês de setembro ainda! Bom, no último artigo, a parte 11, falei sobre como devemos fazer as traduções das medidas de similaridades para funções, considerando a ordem de prioridade de execução dos operadores matemáticos. Hoje, vou mostrar como organizei o projeto para realizar esses cálculos e também algumas novas funções úteis.
REVISITANDO O PROJETO
Antes de começarmos, vamos rever a organização do projeto. Aliás, vocês podem baixá-lo aqui.
Nosso projeto é composto por quatro scripts R:
bibliotecas.R: contém todos os pacotes R necessários para execução do nosso código. Em nosso caso, por hora, os pacotes são progress, tidyverse e dplyr;
similaridades.R: contém todas as medidas de similaridades traduzidas. De acordo com minhas pesquisas, eu consegui elencar 109 dessas medidas, no entanto, existem variações da mesma medida de similaridade. Isto acontece pois existem artigos científicos onde os autores apresentam a mesma medida, mas com uma constituição diferente. Além disso, nesse arquivo há também duas funções diferentes para o cálculo das matrizes de similaridades. Elas são explicadas mais pra frente;
funções.R: contém as funções da matriz de contingência;
principal.R: é o programa principal, onde usamos as funções criadas nos arquivos anteriores!
Pronto! Agora que já nos lembramos do projeto, vamos ver as funções para calcular as matrizes de similaridades propriamente ditas.
CALCULANDO MATRIZES DE SIMILARIDADES
Para não perdermos muito tempo, eu já fiz a tradução de todas as medidas de similaridades. Ainda assim, eu gostaria que vocês olhassem para elas com muita atenção quando forem trabalhar neste projeto. Pode ser que eu tenha errado alguma coisa, afinal sou um ser humano como vocês, também posso errar. Caso encontrem alguma coisa incorreta, por favor, me avisem e então vamos corrigir o problema imediatamente.
Eu havia mencionado que poderíamos calcular uma única medida ou então várias de uma vez só. Então, vamos começar calculando uma medida de similaridade individualmente.
Vamos pegar como exemplo a medida RUSSEL-RAO. Mostrarei aqui três formas diferentes de como podemos escrever uma função para ela:
# VERSÃO 0
russel.rao <- function(a,b,c,d){ return(a/(a+b+c+d)) }# VERSÃO 1
russel.rao.v1 <- function(a,b,c,d,n){return(a/(a+b+c+d))}# VERSÃO 2
russel.rao.v2 <- function(l){return(l$a/(l$a+l$b+l$c+l$d))}
A versão 0 corresponde à versão original, enquanto que as versões 1 e 2 correspondem à adaptações que são necessárias para executar de forma abstrata. Ficou difícil? Então, vamos entender. Lembram do parâmetro FUN? Aquele que nos permite passar uma função como parâmetro? Pois bem, as versões 1 e 2 da função russel.rao são para esta situação. Mas existe uma diferença entre elas, vamos ver:
# MARGIN = C(1,2) indica linha e coluna
# X É UMA MATRIZ
# FUN é a função a ser aplicada
calcula.medida.v1 <- function(rotulos, numero.rotulos, a, b, c, d, n, FUN){
m <- constroi.matriz.similaridade(rotulos, numero.rotulos) # 2
u = (numero.rotulos*numero.rotulos) # 3
pb <- progress_bar$new(total = u) # 4
for (i in 1:numero.rotulos) { # 5
for (j in 1:numero.rotulos) { # 6
m[i,j] = FUN(a[i,j], b[i,j], c[i,j], d[i,j], n[i,j]) # 7
pb$tick() # 8
Sys.sleep(1/u) # 9
gc() # 10
} # fim do for interno # 11
gc() # 12
} # fim do for externo # 13
return(m) # 14
gc() # 15
} # fim da função
# versão abstraída da versão 1
calcula.medida.v2 <- function(Fun, ...) {
Args <- list(...) # 2
Args <- lapply(Args, function(M) apply(X = M, MARGIN = c(1,2),
FUN = as.numeric)) # 2
Fun(Args) # 3
} # fim da função # 4
Na versão calcula.medida.v1 estamos exigindo os parâmetros:
rotulos: que é o espaço de rótulos propriamente dito;
numero.rotulos: que é o total de rótulos que existe no espaço de rótulos em questão;
a, b, c, d, n: que são os elementos básicos da tabela de contingência;
FUN: a função que queremos que seja calculada com a, b, c, d e n, portanto, qual é a medida de similaridade que deve ser calculada.
Na linha # 2 eu estou construindo uma matriz de similaridade que será do tamanho L x L, isto é, se existem 5 rótulos no espaço de rótulos, então teremos uma matriz 5 X 5 = 25.
As linhas # 3 e # 4 apenas lidam com a barra de progresso que vai aparecer no console e já foram explicadas anteriormente. Da linha # 5 até a # 13 nós temos o comando alinhado FOR que calcula a medida e salva o resultado na matriz.
A linha # 7 é quem, de fato, faz o cálculo e note que ali estamos passando os parâmetros a, b, c, d e n para FUN. Quem é FUN? É a função que quisermos na hora de chamar a função. As matrizes a, b, c, d e n serão calculadas dentro dessa função calcula.medida.v1.
Observe que nessa linha, armazenamos o resultado em m[i,j], isto é, FUN é chamada ali com os parâmetros necessários, calcula as matrizes e seu resultado fica na célula correspondente na matriz resultante.
Isso é feito para cada cruzamento de linha e coluna e, por isso, temos o for interno e o for externo. Eu já expliquei sobre isso em outro artigo, recomendo que você volte alguns artigos para relembrar, caso esteja na dúvida.
As linhas # 8 e # 9 apenas lidam com a barra de progresso e o restante das linhas são as finalizações, sendo que a # 14 é a responsável por retornar o resultado à linha chamadora.
Essa é uma forma de se fazer as coisas. Essa função está conectada com a versão 1 do russel.rao e, portanto, a chamada fica assim:
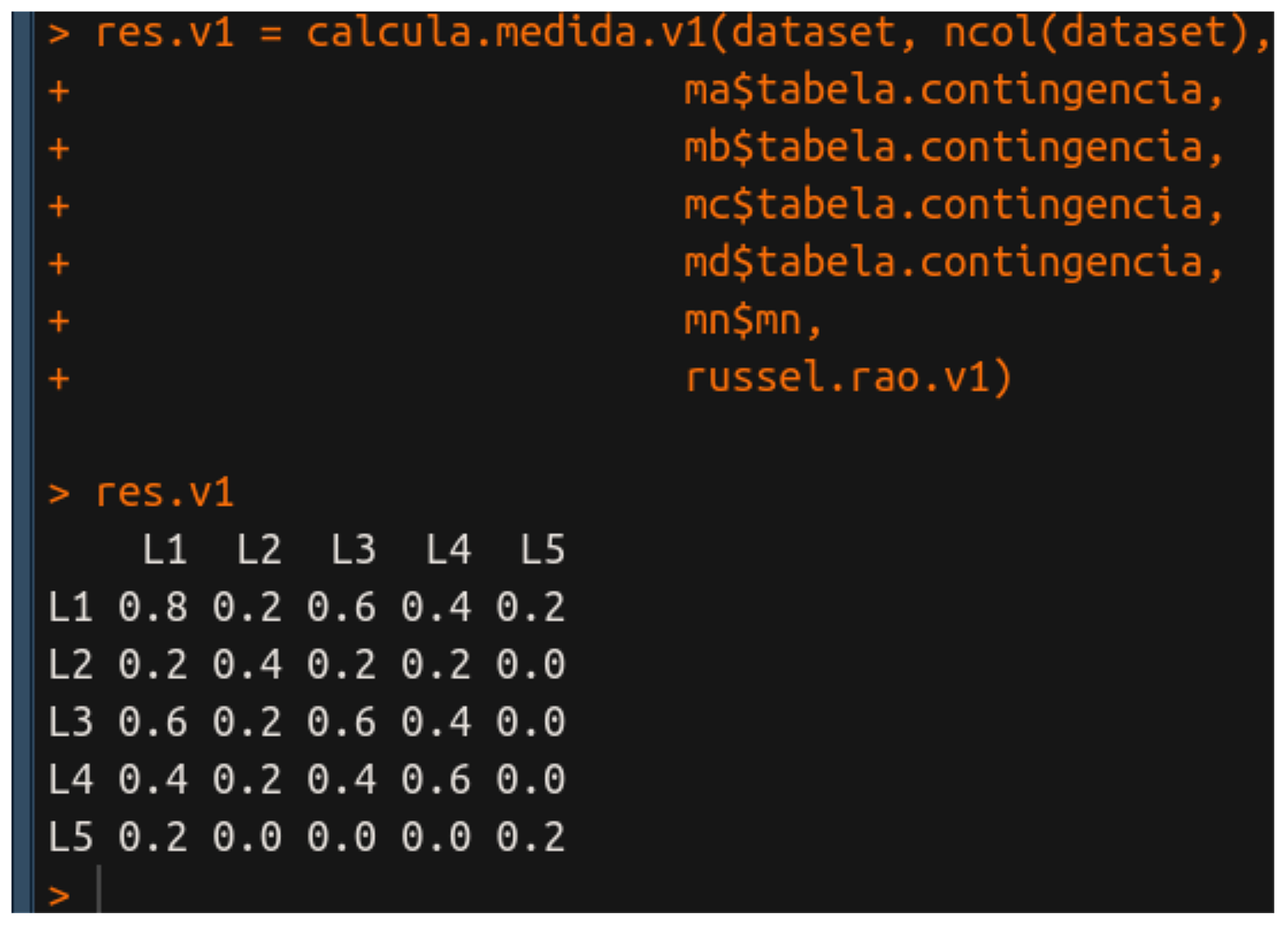
res.v1 = calcula.medida.v1(dataset, ncol(dataset),
ma$tabela.contingencia,
mb$tabela.contingencia,
mc$tabela.contingencia,
md$tabela.contingencia,
mn$mn,
russel.rao.v1)
Notem que precisamos passar o nome da função propriamente dita para que funcione! Ah, e não se esqueçam que, ma$tabela.contingencia e companhia são os resultados calculados anteriormente e aqui são passados como parâmetros. O resultado é:
Legal, né? Vejam que temos a matriz de similaridade certinha! Agora vamos ver a versão 2. Bem, podemos dizer que a v2 é uma abstração da v1. Notem que os parâmetros da função são o FUN e as reticências, então, precisamos passar o nome da função de similaridade e os parâmetros que queremos. As reticências indicam que podemos trabalhar com quantos parâmetros quisermos e isso é muito útil, já que cada medida de similaridade usa elementos diferentes da tabela de contingência.
Na linha # 2 é criada uma variável do tipo lista chamada ARGS. Essa variável basicamente vai pegar os argumentos da função e, por isso, foi dado o nome ARGS, assim facilita também o entendimento. Se passarmos 5 parâmetros, 5 parâmetros serão obtidos, se forem 3, então 3 serão obtidos, e assim por diante.
lapply é uma função que permite aplicar uma função em uma lista de vetores retornando uma lista do mesmo tamanho de X: cada elemento do qual é o resultado da aplicação de FUN ao elemento correspondente de X.
A função apply aplica funções sobre as colunas/linhas (margens) da matriz retornando um vetor, matriz ou lista de valores obtidos aplicando uma função às colunas/linhas de uma matriz.
Em nosso caso, queremos calcular várias medidas de similaridades diferentes (funções) nos elementos da tabela de contingência que são matrizes e, por isso, ambas lapply e apply são utilizadas para fazer abstração da versão 1. Podemos entender o trecho do código abaixo que está dentro de LAPPLY da seguinte forma:
function(M) apply(X = M, MARGIN = c(1,2), FUN = as.numeric)
X é a matriz ou o vetor;
MARGIN é onde queremos que o cálculo seja realizado. Se for apenas a coluna, devemos colocar ali MARGIN=2. Se for apenas a linha, devemos fazer MARGIN=1. Mas se queremos aplicar a função tanto às linhas, quanto às colunas, então fazemos MARGIN=c(1,2);
FUN é a função a ser aplicada na matriz. Vejam que em nosso caso eu coloquei FUN = as.numeric porque vamos usar uma função nossa que deve ser aplicada a números. Aqui não devemos passar o nome da nossa função pois ela já vai ser pega no ARGS e, então, transmitida em function(M).
FUNCTION(M) é a função que queremos de fato, a qual é obtida através de ARGS.
Notem que a linha # 3 é apenas Fun(Args), que é a chamada propriamente dita para realizar o cálculo da função desejada. Para utilizarmos a versão 2, fazemos o seguinte:
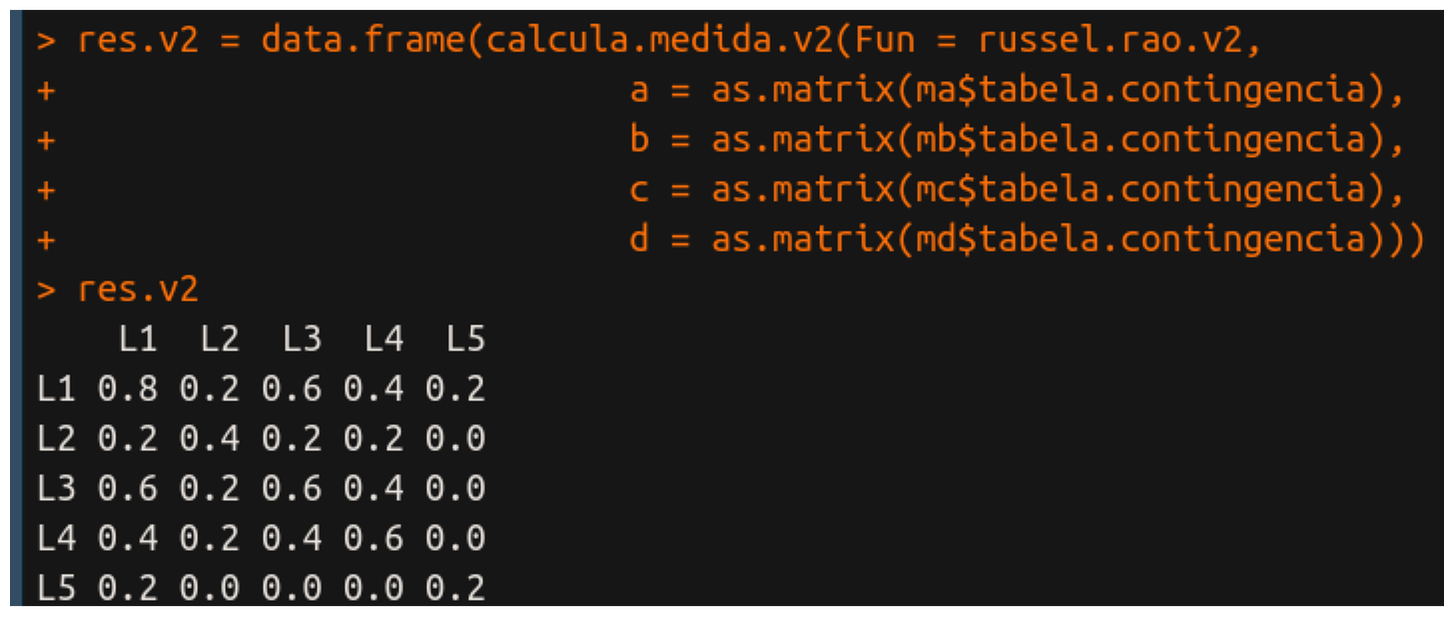
res.v2 = data.frame(calcula.medida.v2(Fun = russel.rao.v2,
a = as.matrix(ma$tabela.contingencia),
b = as.matrix(mb$tabela.contingencia),
c = as.matrix(mc$tabela.contingencia),
d = as.matrix(md$tabela.contingencia)))
Primeiro passamos o nome da função que é russel.rao.v2 e somente depois passamos os parâmetros da tabela de contingência. A principal diferença entre essa versão e a versão 1 é que aqui estamos passando matrizes como parâmetros e elas estão sendo calculadas automaticamente por LAPPLY e APPLY. Na versão 1, a gente faz o cálculo de todas as matrizes necessárias e, portanto, a versão 2 é uma versão abstraída da versão 1.
As funções LAPPLY e APPLY já são automatizadas para realizar esses cálculos de matrizes com mais eficiência, portanto, sempre que possível, tente otimizar o seu código buscando por pacotes do R que permitem isso. Para que o resultado seja apresentado legal no console, eu usei data.frame().
Observem também que a versão 2 de russel.rao exige apenas um parâmetro, que é a letra l, enquanto que na versão 1 exigimos todos os parâmetros na função. Esse parâmetro l é, na verdade, a lista de argumentos a, b, c, e d. O resultado da versão 2 é exatamente igual ao resultado da versão 1:
CONCLUINDO
Pessoal, já estourei o meu limite de espaço neste artigo! Estou finalizando por aqui. No próximo artigo vou retomar esse assunto para finalizarmos a série! Muito obrigada por ter lido até aqui. Nos vamos no próximo artigo.
Este artigo foi escrito por Elaine Cecília Gatto - Cissa e publicado originalmente em Prensa.li.