Classificação Multirrótulo: Calculando Similaridades entre Rótulos - Parte 5
Oi pessoal! Vamos continuar nossa aventura pelo R, RStudio e Classificação Multirrótulo? Vem comigo então.
Recapitulando
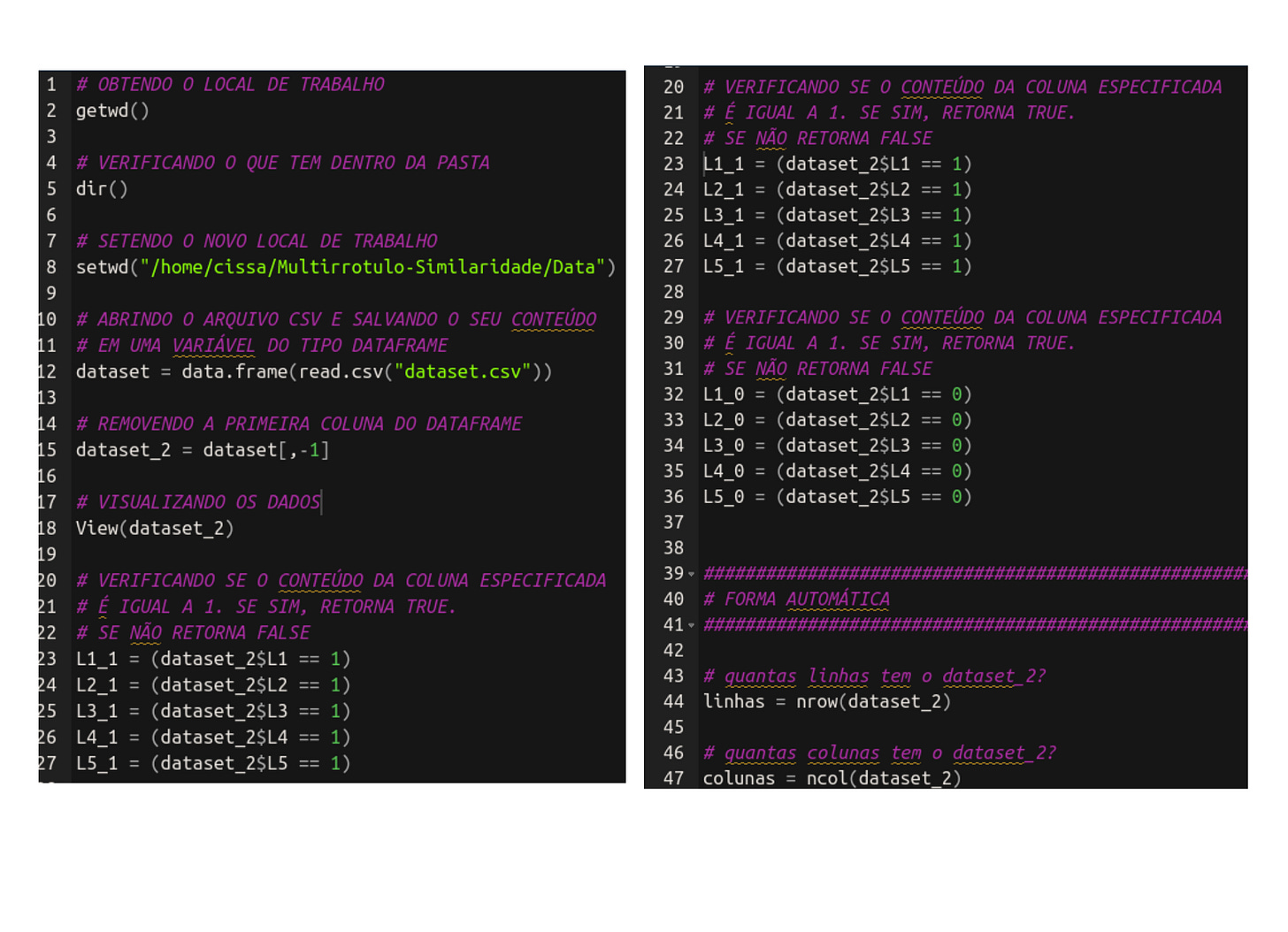
Este é o nosso script R até o momento:
A última coisa que fizemos foi criar a matriz de similaridade! Então vamos continuar dai! Bora lá!!
Funções para a Tabela de Contingência
Para facilitar, vamos criar funções para o cálculo de cada um dos itens da tabela. Essas funções poderão ser chamadas quantas vezes forem necessárias e essa é exatamente a ideia por trás de uma função em programação.
Uma FUNÇÃO deve executar uma tarefa específica de forma objetiva. Além disso, normalmente ela é um trecho de código que pode ser aproveitado por várias partes do seu código.
Portanto, vamos fazer isto para facilitar nosso trabalho! Mas, antes, vamos recapitular os cálculos já que estamos no artigo 5, creio que isto já ficou esquecido.
Vamos calcular a para o rótulo 1 com o rótulo 2. Primeiro vamos separar as colunas correspondentes de cada um deles conforme a seguir:
x = dataset_2$L1
y = dataset_2$L2
A variável x contém os valores do rótulo 1 para todas as instâncias, enquanto que a variável y tem o rótulo 2. Agora vamos verificar onde cada um deles é 1 de fato:
res_x = (x == 1)
res_y = (y == 1)
As variáveis res_x e res_y contém os resultados correspondentes. O próximo passo é verificar quando os dois rótulos estão presentes:
res_x_y = ( (res_x == 1) & (res_y == 1) )
A variável res_x_y contém o resultado. Podemos agora somar:
soma = sum(res_x_y)
E assim temos o valor de a para os rótulos 1 e 2. Esse passo a passo, podemos fazê-lo de uma única vez com a seguinte linha:
a = sum( (x == 1) & (y == 1) )
É essa linha que vai se transformar na nossa função! Os outros cálculos ficam da seguinte forma:
b = sum( (x == 1) & (y == 0) )
c = sum( (x == 0) & (y == 1) )
d = sum( (x == 0) & (y == 0) )
ab = sum(a+b)
ac = sum(a+c)
bd = sum(b+d)
cd = sum(c+d)
ad = sum(a+d)
bc = sum(b+c)
n = a + b + c + d
Todos esses cálculos agora vão se tornar funções! Notem que os cálculos para a, b, c e d precisam de dois parâmetros, o x e o y, enquanto que os outros precisam dos resultados destes.
Uma função é construída da seguinte forma no R:
nome_da_função <- function(parâmetros){
comando_1
comando_2
comando_N
}
Onde parâmetros são valores que temos em alguma parte do nosso código e que queremos que a função use para algo e os comandos são exatamente o que queremos fazer com isso.
Portanto, criei as minhas funções para a tabela de contingência da seguinte forma:
# proporção de 1s que ambas as variáveis compartilham nas mesmas posições
# correspondências positivas entre x e y (x e y == 1)
compute.a <- function(x, y){
return(sum(x == 1 & y == 1))
}
# proporção de 0s em x e de 1s em y nas mesmas posições
# x ausente (x == 0 e y == 1 )
compute.b <- function(x, y){
return(sum(x == 0 & y == 1))
}
# proporção de 1s em x e de 0s em y nas mesmas posições
# y ausente (x == 1 e y == 0)
compute.c <- function(x, y){
return(sum(x == 1 & y == 0))
}
# proporção de 0s que ambas as variáveis compartilham
# correspondências negativas entre x e y (x e y == 0)
compute.d <- function(x,y,m){
return(sum(x == 0 & y == 0))
}
# p1 = a + b --> proporção de 1s em a
compute.ab <- function(a, b){
return(a+b)
}
# p2 = a + c --> proporção de 1s em c
compute.ac <- function(a, c){
return(a+c)
}
# p3 = a + d --> diagonal (11) (00)
compute.ad <- function(a, d){
return(a+d)
}
# p4 = b + c --> diagonal (10) (01)
compute.bc <- function(b, c){
return(b+c)
}
# p5 = b + d --> proporção de 0s em d
compute.bd <- function(b, d){
return(b+d)
}
# p6 = c + d --> proporção de 0s em c
compute.cd <- function(c, d){
return(c+d)
}
# todos
compute.n <- function(a,b,c,d){
return(a+b+c+d)
}
Podemos usar pontos e underline nos nomes das funções. Para ficar bem fácil, usei o nome compute em todas elas, assim sei que estou calculando o valor que desejo. Você também notou um tal de RETURN não é? Pois bem, como o cálculo é de uma única linha, a gente pode colocar ele diretamente no retorno da função.
O que é o retorno? É exatamente isso!!! É o que retorna da função quando a chamamos, em nosso caso, é o resultado da conta que estamos fazendo. Esse resultado pode ser usado onde quisermos desde que ele seja armazenado em uma variável.
Para entender melhor, copie os códigos daqui deste artigo em seu próprio script. Selecione tudo e aperte CTRL+T. Com isto, as funções serão carregadas no seu ambiente de execução, isto signifca que ela estarão disponíveis para serem usadas. Se você não fizer isso, não vai dar pra usá-las, elas estarão lá digitadas, mas não prontas para o uso.
Vou chamar as funções para executar os cálculos para os rótulos 1 e 2:
res_a = compute.a(x,y)
res_b = compute.b(x,y)
res_c = compute.c(x,y)
res_d = compute.d(x,y)
res_ab = compute.ab(res_a, res_b)
res_ac = compute.ac(res_a, res_c)
res_ad = compute.ad(res_a, res_d)
res_bc = compute.bc(res_b, res_c)
res_bd = compute.bd(res_b, res_d)
res_cd = compute.cd(res_c, res_d)
res_n = compute.n(res_a, res_b, res_c, res_d)
Agora vou selecionar todas essas linhas e apertar CTRL+ENTER para que elas sejam executadas. Em seguida, vou ver os resultados de cada uma. Vejam:
Dessa forma, temos os resultados individuais da comparação entre os rótulos 1 e 2 para cada um dos cálculos da Tabela de Contingência. Mas o que precisamos mesmo é fazer isso pra todos os rótulos e por em uma tabela.
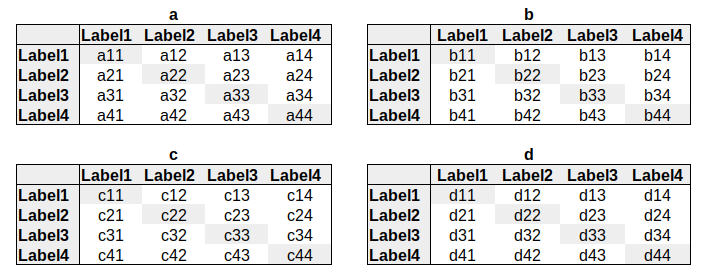
Represento a seguir o que estamos fazendo. Para a é feita a seguinte operação matricial:
Temos uma matriz, que neste exemplo está como 4 x 4, mas não se esqueçam de que a matriz desta série é 5 x 5. Cada coluna e linha é o cruzamento de um rótulo com outro. O resultado que vai na matriz é justamente o resultado do cálculo da nossa função. Esse processo serve para todos os cálculos. Vejam:
Olha a matemática ai! Basicamente o que estamos fazendo é automatizar um cálculo matricial. São variás matrizes que vão sendo calculadas e no final, lá na medida de similaridade específica, vão se transformar em uma só!
Se quiser tirar a prova, você pode efetuar os cálculos na mão para este pequeno dataset. Mas, como sabemos, conforma aumenta o número de rótulos, fica cada vez mais penoso fazer isso na unha!
Finalizando
O artigo de hoje já ficou bem grande e com muita coisa para vocês pensarem!!! No próximo artigo daremos continuidade ao uso de funções para resolver o nosso problema! Baixe aqui o projeto atualizado! Não percam! Espero vocês lá.
Este artigo foi escrito por Elaine Cecília Gatto - Cissa e publicado originalmente em Prensa.li.