Classificação Multirrótulo: Calculando Similaridades entre Rótulos - Parte 8
Olá pessoal! Estou de volta hoje com muito mais coisas novas para mostrar a vocês! Hoje mostrarei um jeito de otimizar ainda mais o código para calcular as probabilidades marginais e a tabela de contingência! Mostrarei também como passar uma função como parâmetro para outra função, e como podemos obter o tempo total gasto na execução de funções. Vamos lá então?!!!
Otimizando ainda mais as funções da tabela de contingência
Bem, no artigo anterior nós criamos uma função para calcular as probabilidades marginais e também criamos uma única função para calcular a tabela de contingência.
No entanto, vocês precisam concordar comigo que ambas as funções fazem um monte de coisas né, e eu falei em artigos anteriores que, idealmente, uma função deve realizar uma tarefa específica. Diante disso, vamos mudar um pouco as coisas, para que a execução seja mais rápida e o código também fique mais bem organizado.
Vamos começar com a tabela de contingência. Seguem as funções para cada um dos diferentes cálculos:
# FUNÇÃO PARA A MATRIZ PARA A
compute.ma <- function(labels, num.labels){
retorno = list()
ma <- build.matrix.sim(labels,num.labels)
u = (num.labels*num.labels)
pb <- progress_bar$new(total = u)
i = 1
j = 1
for (i in 1:num.labels){
for (j in 1:num.labels){
ma[i,j] = compute.a(labels[,i],labels[,j])
pb$tick()
Sys.sleep(1/u)
gc()
}
gc()
}
retorno$ma = ma
return(retorno)
gc()
}
# FUNÇÃO PARA A MATRIZ PARA B
compute.mb <- function(labels, num.labels){
retorno = list()
mb <- build.matrix.sim(labels,num.labels)
u = (num.labels*num.labels)
pb <- progress_bar$new(total = u)
i = 1
j = 1
for (i in 1:num.labels){
for (j in 1:num.labels){
mb[i,j] = compute.b(labels[,i],labels[,j])
pb$tick()
Sys.sleep(1/u)
gc()
}
gc()
}
retorno$mb = mb
return(retorno)
gc()
}
# FUNÇÃO PARA A MATRIZ PARA C
compute.mc <- function(labels, num.labels){
retorno = list()
mc <- build.matrix.sim(labels,num.labels)
u = (num.labels*num.labels)
pb <- progress_bar$new(total = u)
i = 1
j = 1
for (i in 1:num.labels){
for (j in 1:num.labels){
mc[i,j] = compute.c(labels[,i],labels[,j])
pb$tick()
Sys.sleep(1/u)
gc()
}
gc()
}
retorno$mc = mc
return(retorno)
gc()
}
# FUNÇÃO PARA A MATRIZ PARA D
compute.md <- function(labels, num.labels){
retorno = list()
md <- build.matrix.sim(labels,num.labels)
u = (num.labels*num.labels)
pb <- progress_bar$new(total = u)
i = 1
j = 1
for (i in 1:num.labels){
for (j in 1:num.labels){
md[i,j] = compute.d(labels[,i],labels[,j])
pb$tick()
Sys.sleep(1/u)
gc()
}
gc()
}
retorno$md = md
return(retorno)
gc()
}
Para usar as funções, utilize os seguintes comandos:
res_ma = compute.ma(dataset_2, 5)
res_mb = compute.mb(dataset_2, 5)
res_md = compute.md(dataset_2, 5)
res_mc = compute.mc(dataset_2, 5)
Relembrando: dataset_2 é a variável que contém os rótulos e 5 é o número total de rótulos em dataset_2. O resultado que obtemos é exatamente o mesmo se tivéssemos executado a primeira função:
Notem que para cada matriz uma função foi criada e se olharem atentamente, elas são exatamente iguais, a única coisa que muda entre elas, é a função que é chamada dentro dela: compute.a, compute.b, compute.c e compute.d.
Bom, será que tem como automatizar isso aí também? Afinal é um monte de código igual, só muda a função que é chamada, o resto é totalmente igual! Quanto código desnecessário vocês não concordam?
Será que tem algum jeito de passar a FUNÇÃO que queremos como um PARÂMETRO para OUTRA FUNÇÃO? A resposta é sim!!! Colocarei o código primeiro e em seguida explicarei. O nome para isto que estamos fazendo é ABSTRAÇÃO! Estamos abstraindo várias funções em uma única.
compute.cont.table2 <- function(labels, num.labels, FUN){
retorno = list()
m <- build.matrix.sim(labels,num.labels)
u = (num.labels*num.labels)
pb <- progress_bar$new(total = u)
i = 1
j = 1
for (i in 1:num.labels){
for (j in 1:num.labels){
m[i,j] = FUN(labels[,i], labels[,j])
pb$tick()
Sys.sleep(1/u)
gc()
}
gc()
}
retorno$computed = m
return(retorno)
gc()
}
Dei o nome de compute.cont.table2 para esta função. Note que os parâmetros labels e num.labels continuam lá, mas agora tem mais um parâmetro, que é o FUN, que significa FUNÇÃO. Esse parâmetro será o responsável por receber a função propriamente dita e passá-la para dentro da função compute.cont.table2. FASCINANTE NÃO?
O restante da função é praticamente igual ao que fizemos antes, mas o código agora está abstraído, isto é, eu o generalizei para ser capaz de executar para qualquer uma das quatro funções básicas da tabela de contingência. É importante desenvolver essa habilidade de abstração. A princípio pode parecer difícil e chato, mas isso fará a diferença na sua vida de programador. Infelizmente, esse senso não aparece do dia pra noite, é preciso treinar e praticar!
Continuando, observe que agora temos FUN(labels, num.labels) no lugar de compute.a() e etc. FUN será substituido pela função que você passar na chamada da função, veja:
ma3 = compute.cont.table2(dataset_2, 5, compute.a)
mb3 = compute.cont.table2(dataset_2, 5, compute.b)
mc3 = compute.cont.table2(dataset_2, 5, compute.c)
md3 = compute.cont.table2(dataset_2, 5, compute.d)
Agora estamos passando o espaço de rótulos como primeiro parâmetro, o número total do espaço de rótulos como segundo parâmetro, e o terceiro e último parâmetro é a função que você quer que seja executada! BINGO! Conseguimos enxugar ainda mais o nosso código e, ainda por cima, ele executará bem rapidinho!
Falando em tempo, tem um jeito da gente saber quanto tempo foi gasto para executar uma função? Sim!!! Tem sim e é bem fácil, basta usar a função system.time() e dentro dela colocar a nossa chamada de função, da seguinte forma:
system.time(compute.cont.table2(dataset_2, 5, compute.a))
system.time(compute.cont.table2(dataset_2, 5, compute.b))
system.time(compute.cont.table2(dataset_2, 5, compute.c))
system.time(compute.cont.table2(dataset_2, 5, compute.d))
Quando você selecionar essas linhas e executá-las aparecerá o seguinte:
Olha só que interessante! Retornou pra gente esses valores loucos aí. Seus valores provavelmente serão diferentes do meu pois o system.time vai pegar as configurações do seu sistema operacional e também do seu hardware! Como estou executando tudo no linux, esses valores correspondem a milesegundos. O que eles significam?
Usuário é o tempo de CPU gasto pela execução das instruções do usuário do processo chamador. Sistema é o tempo de CPU gasto pelo sistema em nome do processo de chamada. Decorrido é o tempo total que foi gasto. Devemos ler os resultados da seguinte forma onde s = segundos:
usuário: 1.724s, 1.925s, 1.616s e 1.683s
sistema: 0.0s, 0.077s, 0.005s e 0.0s
decorrido: 2.714s, 2.997s, 2.610s e 2.674s
Agora, querem ver algo ainda mais incrível? Vejam essas linhas de código:
time_a = system.time(compute.cont.table2(dataset_2, 5, compute.a))
time_b = system.time(compute.cont.table2(dataset_2, 5, compute.b))
time_c = system.time(compute.cont.table2(dataset_2, 5, compute.c))
time_d = system.time(compute.cont.table2(dataset_2, 5, compute.d))
Estou salvando em variáveis os valores que retornam de system.time(), que ficarão assim agora:
Agora vou converter cada um desses resultados em uma matriz, para que possamos acessá-los diretamente, da seguinte forma:
time_a <- t(data.matrix(time_a))
time_b <- t(data.matrix(time_b))
time_c <- t(data.matrix(time_c))
time_d <- t(data.matrix(time_d))
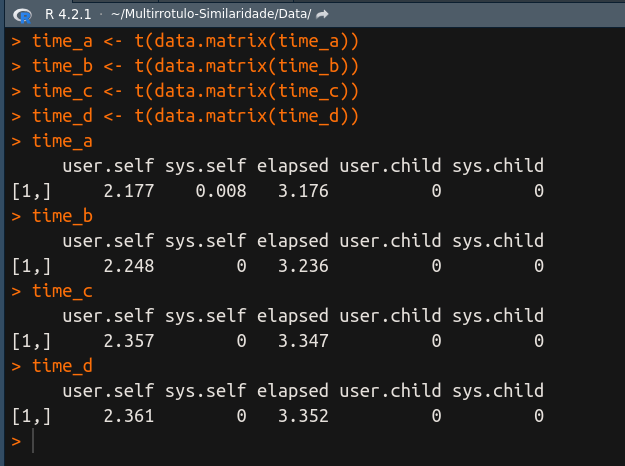
E o resultado que obtemos é:
Notem que ao convertermos para matriz, apareceram outros valores? O que vocês estão vendo ai como USER.CHILD e SYS.CHILD é correspondente a processos filhos que foram executados para os processos de usuário e sistema principais. Normalmente quando o código é paralelizado, e ele executa em várias cores diferentes, então o tempo de execução para cada core vai aparecer ali em CHILD! Interessante né.
UFA! Agora a gente já sabe quanto tempo tá levando pra executar as nossas funções. O que você pode fazer de agora em diante é ir salvando esses tempos e depois juntá-los em um dataframe para verificar o tempo total de execução do script. Algo parecido com isto:
tempo_execucao = rbind(time_a, time_b, time_c, time_d)
FINALIZANDO
Gente, vou parando por aqui! Vou deixar para mostrar a abstração da função de probabilidades marginais no próximo artigo! Espero que vocês estejam gostando dos artigos. A gente se vê no próximo.
Este artigo foi escrito por Elaine Cecília Gatto - Cissa e publicado originalmente em Prensa.li.