Classificação Multirrótulo: Propriedades dos Dados Multirrótulo - Parte 6
Oi, gente! No artigo passado aprendemos a calcular densidade, cardinalidade e as diversas combinações de rótulos presentes no espaço de rótulos. No artigo de hoje vamos aprender novas propriedades.
DOWNLOAD
Antes de começar, faça download do projeto do RStudio, clicando aqui! Abra o projeto em seu computador e não esqueça de verificar se todos os pacotes necessários estão instalados. Eles estão listados no arquivo bibliotecas.R, o qual você deve executar antes de continuar com a leitura deste artigo. Caso tenha dúvidas no processo, consulte este site! Você também pode entrar em contato comigo nas minhas redes sociais.
COMBINAÇÕES DE RÓTULOS ÚNICAS
Agora eu quero saber quantas combinações de rótulos aparecem uma única vez no espaço de rótulos. Para isso, vamos precisar dos resultados do artigo anterior. Vamos lá, sigam a imagens a seguir. Na Figura 1 estou executando novamente o comando para descobrir as combinações.
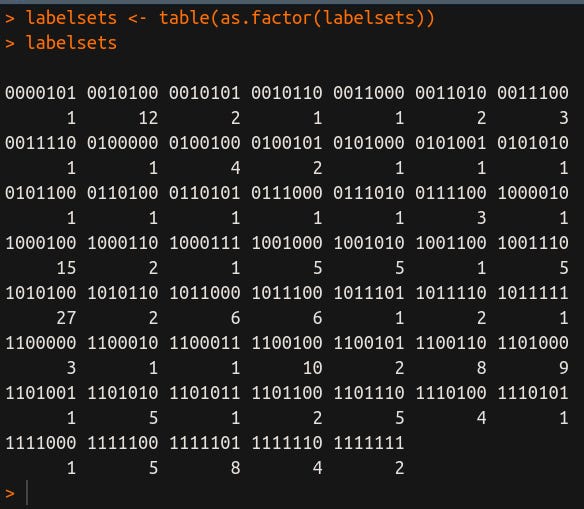
Na Figura 2, executo novamente o comando para gerar a tabela de frequências.
Agora, eu vou converter essa tabela em um dataframe:
Vou, também, trocar os nomes das colunas:
Ótimo, agora fica fácil descobrir quais são as ocorrências únicas. Se uma combinação tem uma frequência igual a 1, então, ela ocorre uma única vez. Aplicando um filtro a gente consegue separar essas combinações, conforme mostra a Figura 5.
Segue aqui o código:
labelsets <- do.call(paste, c(labels, sep = ""))
labelsets <- table(as.factor(labelsets))
labelsets <- data.frame(labelsets)
names(labelsets) = c("combinacao", "frequencia")
labels.sets.unique = filter(labelsets, labelsets$frequencia==1)
NÚMERO TOTAL DE COMBINAÇÕES DE RÓTULOS
Com o dataframe dos labelsets, nós também conseguimos descobrir quantas combinações de rótulos diferentes existem. É bem simples conseguir essa informação, basta pegarmos o número total de linhas do dataframe. Em nosso exemplo, temos 54 combinações diferentes. O código que deve ser executado é o seguinte:
num.total.comb = nrow(labelsets)
NÚMERO TOTAL DE COMBINAÇÕES DE RÓTULOS ÚNICAS
Também é bom sabermos quantas combinações únicas de rótulos existem. O processo é o mesmo do item anterior. Em nosso exemplo, temos 24 combinações únicas e o código a ser executado é o seguinte:
num.total.comb.unique = nrow(labels.sets.unique)
PROPORÇÃO DE COMBINAÇÕES DE RÓTULOS
Nós também podemos calcular a proporção as combinações encontradas. De acordo com o que já fizemos, sabemos que temos 54 combinações diferentes, então isso corresponde a 100%. Temos 24 combinações únicas, portanto, 44,444444444% do espaço de rótulos é composto por essas combinações. 54-24 = 30, portanto, as outras 30 combinações são não únicas, o que corresponde a 55,555555556% do espaço de rótulos.
Dessa análise simples aqui a gente percebe que há uma certa rigidez no espaço de rótulos, no sentido de que a variedade de combinações, apesar de ser muita, não é tão frequente.
COMBINAÇÕES DE RÓTULOS MAIS E MENOS FREQUENTES
Outra informação importante é: quais são as combinações mais frequentes e menos frequentes, tirando aquelas que são únicas? Primeiro, vamos ordenar o dataframe dos labelsets com o comando labels.sets = arrange(labelsets, frequencia). Isso vai colocar as combinações com maior frequência no início do dataframe e as com menor frequência no final, portanto, é uma ordenação crescente.

Agora, nós vamos retirar todas aquelas combinações que são iguais a 1 usando o comando labels.sets = filter(labels.sets, labels.sets$frequencia!=1).
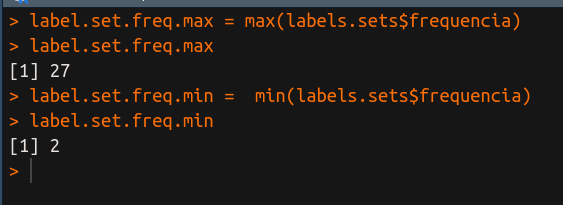
Ótimo, agora usamos os seguintes comandos para descobrir as combinações com maior e menor frequências:
label.set.freq.max = max(labels.sets$frequencia)
label.set.freq.min = min(labels.sets$frequencia)
Com isso, vamos obter que a maior frequência é 27 e a menor 2. Importante ressaltar aqui também que, se o dataset flags tem 7 rótulos, então o número de combinações possíveis de rótulos é muito alto e é totalmente possível que nem todas elas ocorram.
TOTAL DE INSTÂNCIAS ROTULADAS COM UM ÚNICO RÓTULO
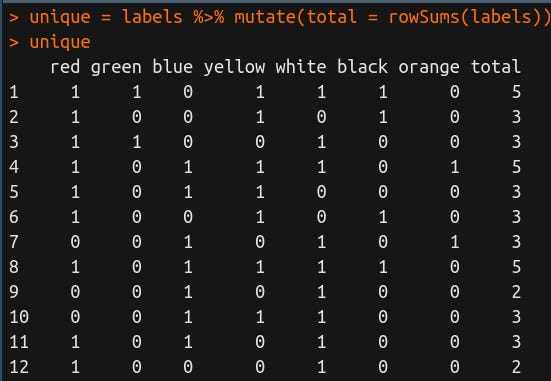
Esta também é outra informação interessante de se obter. Primeiro, vamos calcular quantos rótulos estão ativos em cada instância usando o comando unique = labels %>% mutate(total = rowSums(labels)).
Nesta linha de código eu usei uma função chamada mutate, que tem o objetivo de adicionar uma nova coluna no dataframe. Então, observem que agora tem uma coluna chamada total ali no final. Dentro de mutate eu usei o rowSums que faz justamente a soma de todos os valores da linha. Dessa forma, sabemos quantos rótulos ativos existem em cada instância (linha). Vamos agora ordenar:
Usando arrange() a gente consegue colocar o dataframe em ordem crescente pela coluna total. Agora conseguimos visualizar melhor a informação e já vemos que existe apenas uma instância com um único rótulo ( ~0.51%). Todas as outras instâncias pertencem a mais de um rótulo (~99.5%).
Se por um acaso tivermos muitas instâncias associadas a um único rótulo, é possível que o classificador multirrótulo tenha dificuldades no aprendizado, já que o dataset está se configurando mais como um problema binário do que multirrótulo. Pode ser que os resultados para o dataset em questão sejam mais acurados se um classificador simples-rótulo for usado.
TOTAL DE INSTÂNCIAS ROTULADAS COM MAIS DE UM RÓTULO
É legal agora também usarmos o count() para calcular quantas instâncias pertencem a 2 ou mais rótulos, independente de quais sejam esses rótulos:
frequência = data.frame(count(unique, total))
names(frequencia) = c("total", "frequencia")
Olhem só que interessante! Só tem uma instância que pertence a um único rótulo e as instâncias que pertencem a 3 rótulos são a maioria (76). As instâncias que pertencem a 2 rótulos e 4 rótulos têm quase a mesma frequência, 43 e 44 respectivamente.
Notem que só temos 2 instâncias que pertencem a todos os rótulos! Instâncias que pertencem a 5 e 6 rótulos também têm uma frequência parecida, 15 e 13 respectivamente. Parece que não, mas este tipo de análise pode nos trazer muitos insights e ajudar até mesmo a avaliar os resultados de um classificador.
FINALIZANDO
Muito obrigada por ter lido até aqui! Aprendemos bastante neste artigo, né? Para não ficar muito cansativo vou parando por aqui. No próximo artigo vou apresentar mais algumas propriedades e, então, vamos começar a arrumar o novo projeto! Até lá.
Este artigo foi escrito por Elaine Cecília Gatto - Cissa e publicado originalmente em Prensa.li.